※本記事は、Mahmoud Abdelghanyによる”Is it time for operator overloading in Java?“を翻訳したものです。
賛否が両極端に分かれる演算子オーバーロード。本記事は、コードの読み書きとデバッグを簡単にするために演算子オーバーロードは欠かせないと主張する
著者:Mahmoud Abdelghany
2020年6月8日
演算子オーバーロードは一風変わった言語機能の1つで、賛否が両極端に分かれます。強く否定する意見があるのもうなずけます。演算子オーバーロードの利用方法が適切でなければ、たちまちコードはわかりにくくなり、さらに厄介なバグが生まれることになるからです。本記事では、算術演算のプログラミングを題材に、強く支持する意見を簡単に述べたいと思います。
まず、用語を定義するために、ISOのC++ Wikiを確認してみます。そこには、「演算子オーバーロードにより、C/C++のユーザー定義型(クラス)における演算子の意味をユーザーが定義できるようになります。オーバーロードされた演算子は、関数呼出しのシンタックス・シュガーです」と書かれています。
つまり、クラスFooを定義した場合、FooBar = Foo + Bar;のようなプラス演算子の実装も定義できるということです。
演算子オーバーロードは、それほど重要でない言語機能だと一般的に考えられています。シンタックス・シュガーとは、このような事象を表すためにもっともよく使われる用語です。先ほどの定義で、シンタックス・シュガーという部分は正しい記述です。ほぼすべてのプログラミング言語には、シンタックス・シュガーの抽象化が含まれており、複雑な機械語のコードを実際には書かなくても、それに相当する処理を書くことができます。
この点を踏まえて、Javaの世界で演算子オーバーロードがたびたび忌み嫌われている理由の1つ目について見てみます。その最大の理由は、cout<<にあります。この問題は、<<演算子に象徴されます。次のC++文では、この演算子が適切にオーバーロードされています。
cout<<"what the #@$#"<<endl;
この文は、次の文と同じ意味です。
System.out.println("what the #@$#");
ここでは、対象を左にシフトしているのではなく、標準出力(通常はコンソール)を意味するcoutに文字列を渡しています。
C++などの言語では、カンマなどの見慣れない演算子をオーバーロードすることができます。不思議なことに、これにも用途があります。さらに、独自の演算子を定義できる言語も存在します。これにも興味深い用途があるのですが、Javaでの演算子オーバーロードの価値について説明する本記事の範囲を超える内容です。
見慣れぬ演算子のオーバーロードはさておき、実情としては、誰かがオーバーロードした演算子を使う場合、実行される演算がその演算子の数学的目的と一致しているという保証はもはや存在しません。
最初に挙げた例、FooBar = Foo + Bar;について考えてみます。
- +演算子が加算に似た操作を実際に行うということは、どうすればわかるか
- 演算によってFooやBarが変更されたらどうなるか
- また、実行するたびに、単にランダムなFooBarが返されたらどうなるか
- 副作用はどうか
これらはすべて的を射た質問ですが、実は演算子オーバーロードに限った話ではありません。先ほどの式を、次のように書き換えたとします。
FooBar = Foo.plus(Bar);
このように変更したからといって、何か別のことが保証されるというわけではありません。演算子オーバーロードに関して考えられる弊害のほとんどは、メソッドの世界でも大して変わりません。その理由を20ページにわたって書き連ねることもできますが、本記事では、Javaに演算子オーバーロードを導入する準備は整っているのか、そして、演算子オーバーロードはどのように役立つ可能性があるのかという2つの問いに答えることに主眼を置きます。まずは、2番目の問いに答えるところから始めます。
演算子オーバーロードは役に立つのか、そうであればどのように役立つのか
少しの間、次のコードを眺めてみてください。どのような意味だと思うでしょうか。
final BigDecimal result = a.multiply(x.pow(2)).plus(b.multiply(x.plus(c)));
図1のような標準形の2次方程式だと答えた方は、ほぼ正解です。
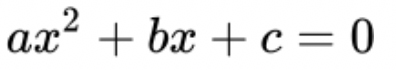
図1:2次方程式
それでは、演算子オーバーロードを使った場合、どんなコードになるでしょうか。次のようなコードになって読みやすくなるでしょう。
final BigDecimal result = a * (x * x) + b * x + c;
もう少し複雑な例を見てみます。この2次方程式からxを求めたい場合、変形や整理などを行って、図2のようにします。
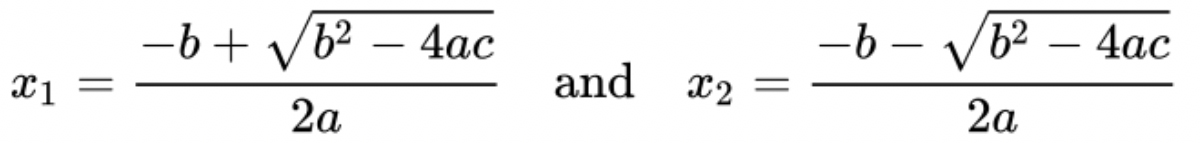
図2:方程式の解
演算子オーバーロードを使用せずに、BigDecimalを使用したコードでこの解を表した場合、どのようになるでしょうか。
final BigDecimal sqrt = b.pow(2).min(a.multiply(c).multiply(4)).sqrt(); final BigDecimal x1 = b.negate().plus(sqrt).divide(a.multiply(2));
演算子オーバーロードを使用した場合、次のコードになります。
final BigDecimal sqrt = (b * b - 4 * a * c).sqrt(); final BigDecimal x1 = (-b + sqrt) / (2 * a);
これは好みの問題ですが、多くどころか、おそらくほとんどの開発者は、演算子オーバーロードを用いたものの方が読みやすく、書きやすく、検証しやすいとわかるのではないかと思います。
書きやすいということについて言えば、コードで抽象化が使われる理由には、読みやすさと書きやすさという両方があります。a.multiply(b).multiply(4)よりも、4*a*cの方がはるかに書きやすいというのが筆者の考えです。シンプルにもなっているため、バグが入り込む余地が小さくなっています。
バグへの影響
謝らなければならないことがあります。実は、本記事の最初の例にはバグがあります。おそらくこれは、筆者自身も含め、ほとんどの方が見逃してしまうようなものでしょう。ヒントを出すために、演算子オーバーロードを用いた方にもバグが含まれるように書き換えてみます。そうすれば、バグはほぼ一瞬で明らかになります。
final BigDecimal result = a * (x * x) + b * (x + c);
このバグは、演算子の優先順位が間違っているという単純なものです。演算子オーバーロードを使えばすぐに明らかになりますが、問題を引き起こすという点はいずれのコードも同じです。
さらにわかりにくいバグとして、ユーザー定義型の推移的結合があります。ただしこのバグは、演算子オーバーロードを使ってその解釈をコンパイラに任せれば、何もしなくても解決します。次の例について考えてみます。
class Vector{ float x, y, z; }
final Vector result = vec1 + vec2 + vec3;
final Vector result = vec1.plus(vec2.plus(vec3));
1,000回のうち999回は、いずれの行も同じ結果になるでしょう。しかし、結果が異なる場合もあります。その理由は、演算子の優先順位にあります。
a + b + cとc + b + aに違いがあるのかと思う方もいるかもしれません。これらの演算には結合法則が成り立つのではないでしょうか。
現実の世界ではそうですが、デジタルの世界では状況次第です。
ご覧のとおり、Vectorクラスには3つの決まった浮動小数点数が含まれています。バイナリの浮動小数点演算では、バイナリ値で表現できる、一番近い値が演算の結果となります。そのため、a.x + b.x = 0.23548787だった場合、32ビット幅の値しかなく、すべての小数を正確に表せるわけではないため、コードの結果が0.2354877Fになる可能性があります。
この情報をコードに適用すると、a + bは近似値となることがわかります。その後、この数はcと加算され、さらに別の近似値が生成されます。
そのため、コードの実行によって不可逆変換が起きる可能性があるため、逆順で同じ計算を行っても結合法則は成立しません。この点は、IEEE浮動小数点演算基準にも記載されています。ほとんどの場合、アプリケーションが表現可能な小数を使っていたり、開発者が損失を気にしなかったりするため(画面のグラフィック計算を行う場合など)、結果は一致することになります。次に例を示します。
final float a = 3.3333333f; final float b = 0.6373606f; final float c = 0.36263946f; System.out.println(a + b + c);//4.3333335 System.out.println(c + b + a);//4.333333
通常、演算を間違った順序で書いた場合や、不適切な括弧を追加した場合、演算子オーバーロードを用いてもこのバグは発生します。しかし、閉じ括弧の位置が前すぎたり後すぎたりするという基本的なバグは、不思議なくらいきれいになくなります。
訂正として、バグのないコードを次に記しておきます。
final Vector result = vec1.plus(vec2).plus(vec3);
演算子オーバーロードを用いずに何らかの計算を行わなければならない場合、こういった種類のバグはとてもよく見られます。その理由は、関数がこのような呼び出され方を想定して作られたものではないからです。学校で代数を習った私たちの脳も、そのように働くものではありません。
James Gosling氏は、「The Evolution of Numerical Computing in Java」(Javaの数値計算の進化)で次のように述べています。「私が知る数値演算を行っている人はすべて、演算子オーバーロードは絶対に欠かせないと主張している。式をメソッド呼出し形式で書くのは、あまりにも不格好で実質的に役に立たない」
演算子について、もう1つ興味深い事実があります。演算子は、それが起こす可能性のある副作用について表現できるということです。言葉を換えれば、プラス演算子は定義上、2つのオペランドを加算し、どちらのオペランドも変更せずに結果を生成します(ただし、ほとんどの言語はプログラマーが演算子をオーバーロードするときに何でも認めてしまうため、必ずそうなるという保証はありません)。明らかな例は、Stringのプラス演算子のオーバーロードです。しかし、plusメソッドには何の前提もありません。メソッドは、望むことが何でもできるものとして理解されているからです。
プログラマーにとってはこちらの方がはるかにおもしろいかもしれませんが、演算子が読取り専用の演算を行うことがわかれば、コンパイラは強力な最適化を行えるようになります。
Javaに演算子オーバーロードを導入する準備は整っているのか
この問いかけを行うということは、自ら墓穴を掘るようなものでしょう。というのも、これに回答するのはほぼ不可能だからです。そこで、ニーズとメリットについて考えてみることにします。興味深いことに、データ解析や金融取引の分野でJavaアプリケーションの使用が増えるに従って、このニーズはいつの間にか急上昇しています。このような分野では、高度な数式が多用されています。
もう1つの興味深い点は、ゲーム分野の発展です。すべてJavaで書かれたMinecraft(歴史上特によく売れたゲームの1つ)が登場したことは、ゲームの分野でもJavaは他の最高の作品と肩を並べることができるという証になりました。もちろん、3Dゲーム・エンジンはすてきな代数学と幾何学の集合体でしかありません。
Clojure、Groovy、Kotlin、ScalaなどのJVM言語は、すべて何らかの形で演算子オーバーロードを実装しています。この点も、Javaコミュニティがそのような発展に対してオープンであることを示す明らかな印だと考えることができるでしょう。
Project Valhallaでは、Java開発者にvalue型が提供される予定です。これは、プリミティブタイプのように振る舞うユーザー定義オブジェクトです。つまり、int64やunsigned_int32といった型を独自に定義できるようになるということです。ただし、この新たな値型に対して関数呼出しで演算を行わなければならないというのは、残念なことです。演算子オーバーロードにとって、値型は完璧なユースケースになると考えられます。
補足ですが、一部のプロセッサ・アーキテクチャでは、int64がCPUレジスタに収まります。つまり、64ビット命令を使った算術演算を行う際のJVM最適化をさらに進めることができます。Javaに演算子オーバーロードや、特定の関数が追加型(64ビット幅整数など)の算術演算を行うものであることを示す何らかの仕組みがあれば、この処理は簡単になります。
まとめ
存在するすべての言語機能やライブラリは、諸刃の剣となる可能性を秘めています。起きる被害が明らかなので回避しやすい機能もあれば、わかりにくく見慣れないため被害を回避しにくい機能もあります。
ベスト・プラクティスが導入される理由は、被害を最小限にとどめ、未知の被害について開発者を啓蒙するためです。その点に関して言えば、演算子オーバーロードも例外ではありません。数学的な問題のプログラムを書いたり、そのエラーをデバッグしたりするときに適切に使えば、とても便利なツールになり、多くの時間を節約することができます。つまり、開発者が無駄にする時間が少なくなり、解決しようとしている実際の問題に費やせる時間が増えることになります。
 |
Mahmoud AbdelghanyMahmoud Abdelghany:Javaテクノロジーを専門とするオランダのコンサルティング会社Blue4ITのエンジニア。多くの時間を費やしてゲームを研究することがきっかけとなり、1年の大部分をかけて演算子オーバーロードについて調査している。Twitterのフォローはこちらから。 |
