Spatial trajectory data is becoming increasingly important in various fields, including transportation, ecology, sports analytics, and even human mobility studies. The ability to compare and measure the similarity of these trajectories can help in applications like identifying common travel patterns, detecting anomalies in movement, or optimizing routes based on historical data. A regular spatial data cleansing exercise involves matching tracks created from noisy, or slightly inaccurate, GPS data to known roads or paths.
In this blog post, we will explore how to use MySQL’s spatial features to analyze the similarity of trajectories. We will focus on key metrics such as Frechet distance (MySQL’s function ST_FrechetDistance), which measures the similarity between two trajectories, and other geometric operations that help quantify how closely different paths align.
This functionality is available in MySQL Community and Enterprise Editions and HeatWave MySQL.
Analysing walk trajectories in a park
Consider the problem of analyzing the movement of walkers in a city park. In this example, we represent each walker’s trajectory as a LINESTRING. Let’s assume we have GPS data for the walkers collected over a period of time. Transforming GPS data into trajectories is presented in this blog post. First we create the table to hold the data:
CREATE TABLE walk_trajectories (
id INT AUTO_INCREMENT PRIMARY KEY,
walker_name VARCHAR(100),
trajectory LINESTRING NOT NULL SRID 4326
);
Note that the GPS trajectories are represented using the WGS 84 geographic coordinate system (represented by SRID 4326). For more on spatial reference systems and SRIDs we refer to a previous blog post.
Then we insert the GPS data in our table:
INSERT INTO walk_trajectories (walker_name, trajectory) VALUES
('Red Walker', ST_GeomFromText('LINESTRING(37.79562087383118 -122.46702694852982,37.7956012 -122.4670506,37.7955599 -122.4671136,37.7955243 -122.4671745,37.7954966 -122.4672255,37.7954759 -122.4672803,37.7954534 -122.4673499,37.7954181 -122.4674723,37.7953104 -122.4679047,37.7952792 -122.4680356,37.7952403 -122.4681458,37.795211 -122.4682021,37.7951776 -122.4682513,37.7951367 -122.468302,37.7950253 -122.468414,37.794974 -122.468481,37.794909 -122.468587,37.794877 -122.468668,37.794855 -122.468769,37.794852 -122.468904,37.7948625 -122.4689824,37.794888 -122.469046,37.7949726 -122.4691719,37.795056 -122.469263,37.7951199 -122.4693423,37.7951531 -122.4693115,37.7952016 -122.469269,37.795257 -122.4692223,37.7952906 -122.4691971,37.7953097 -122.4691838,37.7953481 -122.4691595,37.7953838 -122.4691424,37.7954199 -122.469131,37.795457 -122.4691254,37.7954934 -122.4691247,37.7955311 -122.4691268,37.7955659 -122.4691335,37.7956027 -122.4691418,37.795629 -122.4691489,37.7956738 -122.4691624,37.7957277 -122.469183,37.7957798 -122.4692086,37.7958306 -122.4692375,37.7958781 -122.4692629,37.7959215 -122.4692814,37.7959695 -122.4692929,37.7960161 -122.4692933,37.7960564 -122.4692831,37.7960939 -122.4692659,37.7961254 -122.4692411,37.7961532 -122.4692115,37.7961741 -122.4691849,37.7961938 -122.469152,37.7962897 -122.4689668,37.7963355 -122.4688798,37.7963845 -122.4687902,37.7964298 -122.4687122,37.7964824 -122.4686279,37.7965342 -122.4685538,37.7965849 -122.4684856,37.7966363 -122.4684182,37.7966796 -122.4683636,37.796737 -122.4682994,37.7968009 -122.4682335,37.7968656 -122.4681718,37.7971681 -122.4678909,37.7972322 -122.4678313,37.7972714 -122.4677967,37.7973108 -122.467765,37.7973526 -122.4677401,37.797394 -122.4677221,37.7974527 -122.4677091,37.7975103 -122.4677104,37.7975635 -122.4677251,37.7976099 -122.4677465,37.7976599 -122.4677815,37.7977004 -122.4678246,37.7977382 -122.4678928,37.7977657 -122.4679639,37.7977847 -122.4680304,37.7979263 -122.4686621,37.7979524 -122.4687553,37.797978 -122.4688301,37.7980072 -122.4688995,37.7980396 -122.4689606,37.7983457 -122.4686602,37.7984301 -122.4685586,37.7984665 -122.4685136,37.798519 -122.468456,37.79858158135988 -122.46840682510111)', 4326));
INSERT INTO walk_trajectories (walker_name, trajectory) VALUES
('Orange Walker', ST_GeomFromText('LINESTRING(37.79482108844495 -122.4645294833186,37.794799 -122.464502,37.794626 -122.464206,37.794467 -122.463968,37.794485 -122.463823,37.794555 -122.463591,37.794643 -122.46339,37.794732 -122.463321,37.7947455 -122.463375,37.7947782 -122.4635064,37.794867 -122.463863,37.7949197 -122.4639853,37.7949857 -122.4640935,37.7950715 -122.464169,37.7951561 -122.4642276,37.7953511 -122.4643412,37.7953905 -122.4643701,37.7955512 -122.4645025,37.7956021 -122.4644328,37.7956434 -122.4644212,37.7957046 -122.464439,37.7959564 -122.4645123,37.7961988 -122.4645231,37.7962859 -122.4644272,37.7964012 -122.4643843,37.7964096 -122.4643814,37.7965165 -122.4643499,37.7965776 -122.4643499,37.7966589 -122.4643671,37.7967471 -122.4644358,37.796774 -122.4644811,37.796841 -122.464411,37.7969942 -122.4644235,37.797037 -122.464427,37.797102 -122.464466,37.797172 -122.464572,37.797195 -122.464787,37.797263 -122.4649764,37.7972974 -122.4651364,37.797379 -122.465304,37.797378 -122.465444,37.797392 -122.465536,37.797488 -122.46579,37.797533 -122.465968,37.797576 -122.466433,37.797563 -122.466525,37.79748 -122.466678,37.797468 -122.466768,37.797506 -122.466997,37.7976 -122.467159,37.7976769 -122.4671803,37.7977357 -122.4672502,37.7977634 -122.4673603,37.7977709 -122.4673781,37.797736 -122.4675416,37.7977094 -122.4676502,37.7977004 -122.4678246,37.7977382 -122.4678928,37.7977657 -122.4679639,37.7977847 -122.4680304,37.7979263 -122.4686621,37.7979524 -122.4687553,37.797978 -122.4688301,37.7980072 -122.4688995,37.7980396 -122.4689606,37.7979617 -122.4690293,37.797899 -122.4691154,37.7978717 -122.4690874,37.7978485 -122.4690684,37.7978194 -122.4690588,37.7977902 -122.469064,37.7977491 -122.4690918,37.7977106 -122.469139,37.7976752 -122.4691978,37.7976453 -122.4692561,37.7976175 -122.4693151,37.79759 -122.4693831,37.7975464 -122.4694971,37.7975118 -122.4695889,37.7975004 -122.4696329,37.7974951 -122.469679,37.7974932 -122.4697222,37.797495 -122.4699267,37.7975004 -122.4699808,37.797506559515654 -122.47000914467381)', 4326));
INSERT INTO walk_trajectories (walker_name, trajectory) VALUES
('Blue Walker', ST_GeomFromText('LINESTRING(37.795951956800835 -122.46451100656672,37.7959564 -122.4645123,37.7961988 -122.4645231,37.7962859 -122.4644272,37.7964012 -122.4643843,37.7964096 -122.4643814,37.7965165 -122.4643499,37.7965776 -122.4643499,37.7966589 -122.4643671,37.7967471 -122.4644358,37.796774 -122.4644811,37.796841 -122.464411,37.7969942 -122.4644235,37.797037 -122.464427,37.797102 -122.464466,37.797172 -122.464572,37.797195 -122.464787,37.797263 -122.4649764,37.7972974 -122.4651364,37.797379 -122.465304,37.797378 -122.465444,37.797392 -122.465536,37.797488 -122.46579,37.797533 -122.465968,37.797576 -122.466433,37.797563 -122.466525,37.79748 -122.466678,37.797468 -122.466768,37.797506 -122.466997,37.7976 -122.467159,37.7976769 -122.4671803,37.7977357 -122.4672502,37.7977634 -122.4673603,37.7977709 -122.4673781,37.7977815 -122.4673889,37.7978012 -122.4673898,37.7978124 -122.4673731,37.7978217 -122.4671592,37.7979107 -122.4670819,37.7979545 -122.4671,37.7979791 -122.4671624,37.7980287 -122.4672285,37.7980584 -122.4672983,37.798062 -122.467368,37.7980572 -122.4675702,37.7980594 -122.4677186,37.798026 -122.467992,37.7980211 -122.4681211,37.7980226 -122.4681609,37.7980747 -122.4682775,37.7980892 -122.4683561,37.7981142 -122.4683971,37.7981561 -122.4684234,37.7983493 -122.4684585,37.7983795 -122.4684881,37.7984301 -122.4685586,37.7984665 -122.4685136,37.798519 -122.468456,37.7986357 -122.4683643,37.7986936 -122.4682506,37.7987175 -122.4681369,37.7987255 -122.4680383,37.7987186 -122.4679823,37.79869201265307 -122.46791956856391)', 4326));
INSERT INTO walk_trajectories (walker_name, trajectory) VALUES
('Green Walker', ST_GeomFromText('LINESTRING(37.79479601418929 -122.46357793761146,37.794867 -122.463863,37.7949197 -122.4639853,37.7949857 -122.4640935,37.7950715 -122.464169,37.7951561 -122.4642276,37.7953511 -122.4643412,37.7953905 -122.4643701,37.7955512 -122.4645025,37.7956021 -122.4644328,37.7956434 -122.4644212,37.7957046 -122.464439,37.7959564 -122.4645123,37.7961988 -122.4645231,37.7964195 -122.4644959,37.7965414 -122.4644814,37.7966339 -122.4645057,37.7966842 -122.4645444,37.7967399 -122.4646324,37.7967468 -122.464753,37.7967138 -122.4650008,37.7966523 -122.465259,37.7966115 -122.4655337,37.7965474 -122.4663887,37.7965157 -122.466681,37.7964589 -122.466942,37.7963396 -122.4669996,37.7962695 -122.467098,37.7962504 -122.4671278,37.7962169 -122.4671802,37.7961796 -122.4672275,37.796151 -122.467292,37.7956588 -122.4689369,37.7956419 -122.4689849,37.7956291 -122.4690289,37.7956147 -122.4690867,37.7956027 -122.4691418,37.7956532 -122.4692212,37.7957024 -122.4692982,37.7957261 -122.4693958,37.7957216 -122.469482,37.7957242 -122.4695602,37.7957464 -122.4696513,37.7957727 -122.4697368,37.795893 -122.470146,37.796021 -122.470426,37.796307 -122.470781,37.796682 -122.471141,37.797249 -122.471761,37.797406 -122.47188,37.797654 -122.472134,37.797802 -122.472393,37.79787 -122.472616,37.797888 -122.472847,37.797899 -122.472949,37.79791649714564 -122.47311959717)', 4326));
The Frechet distance is a mathematical way to measure the similarity between two curves, considering not just their shape but also the way they are traversed. It is often used to compare spatial trajectories. In MySQL, the ST_FrechetDistance function computes the Frechet distance between two trajectories. This function is perfect for our use case as it accounts for the path’s geometric shape and its traversal order.
We can compare how similar are the stored trajectories with respect to a fixed trajectory, say the first one.
SELECT walker_name, id, ST_FrechetDistance(trajectory, (SELECT trajectory FROM walk_trajectories WHERE walker_name='Red Walker')) as similarity FROM walk_trajectories; +---------------+----+--------------------+ | walker_name | id | similarity | +---------------+----+--------------------+ | Red Walker | 1 | 0 | | Orange Walker | 2 | 340.99002878471487 | | Blue Walker | 3 | 342.0596889960262 | | Green Walker | 4 | 421.5789953668151 | +---------------+----+--------------------+ 4 rows in set (0,01 sec)
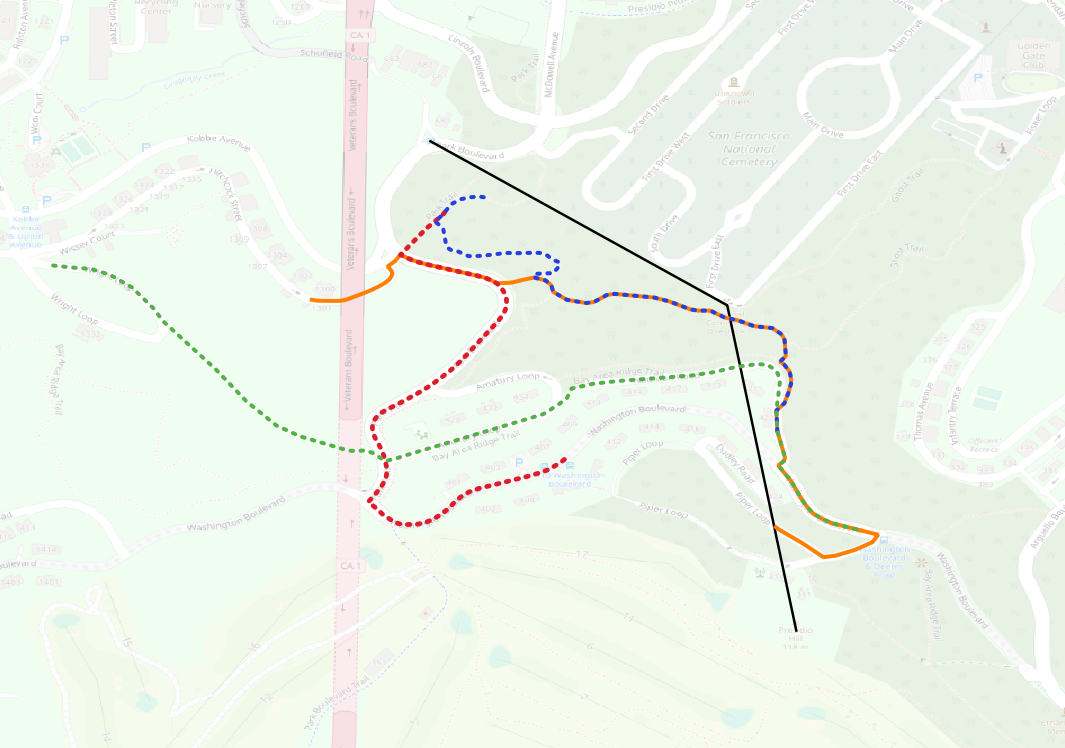
Now assume that we start from the Presidio Hill (POINT(37.79360088412314 -122.46428847312926)) and we want to visit the National Cemetery Overlook (POINT(37.79744139891328 -122.46510386466979)) and end up to Park Boulevard and Shofield bus station (POINT(37.79937853647067 -122.46860817074773)). We can query our trajectory table to find the most similar trajectory to our desired route. Our route can be modelled as
LINESTRING(37.79360088412314 -122.46428847312926,37.79744139891328 -122.46510386466979,37.79937853647067 -122.46860817074773)
that connects all the points of interest we want to visit (depicted with black color in the map above). Then our query can be written as:
SELECT walker_name, id,
ST_FrechetDistance(trajectory,
ST_GeomFromText('LINESTRING(37.79360088412314 -122.46428847312926,37.79744139891328 -122.46510386466979,37.79937853647067 -122.46860817074773)', 4326))
as similarity
FROM walk_trajectories
ORDER BY similarity;
+---------------+----+--------------------+
| walker_name | id | similarity |
+---------------+----+--------------------+
| Orange Walker | 2 | 241.65190882342154 |
| Blue Walker | 3 | 261.68893003364565 |
| Green Walker | 4 | 429.19109867209164 |
| Red Walker | 1 | 453.59273618286403 |
+---------------+----+--------------------+
4 rows in set (0,00 sec)
That is, the most similar trajectories to our query linestring are the orange and the blue.
Lastly, we want to run a slightly different query. Observe that the trajectories have overlaps. We want to find the two trajectories with the largest overlap, as a different measure of similarity. The following query performs this task:
SELECT t1.walker_name,t2.walker_name, ST_Length(ST_Intersection(t1.trajectory, t2.trajectory)) as common_length FROM walk_trajectories t1 CROSS JOIN walk_trajectories t2 ON t1.id < t2.id ORDER BY common_length DESC; +---------------+---------------+--------------------+ | walker_name | walker_name | common_length | +---------------+---------------+--------------------+ | Orange Walker | Blue Walker | 423.1932792589895 | | Orange Walker | Green Walker | 172.44142700478628 | | Red Walker | Orange Walker | 107.59951501720846 | | Blue Walker | Green Walker | 26.921615355894808 | | Red Walker | Blue Walker | 13.384680833787076 | | Red Walker | Green Walker | NULL | +---------------+---------------+--------------------+ 6 rows in set (0,00 sec)
The CROSS JOIN will return all the possible pairs of trajectories (without repetitions) and then we sort according to the length of the common intersection of the pair. The length is computed by MySQL spatial function ST_Length while the intersection is computed by MySQL spatial function ST_Intersection. The result (also visible in the map) shows that the two trajectories with the most overlap are the orange and the blue.
Summary
MySQL’s spatial functions provide a robust toolkit for analyzing and comparing spatial trajectories. By leveraging metrics like Frechet distance, distance/length, and spatial set operations (e.g. linestring intersections), you can perform in-depth comparisons of movement patterns, whether you’re analyzing GPS data, transportation routes, or wildlife movement.
These functions open up powerful possibilities for understanding spatial data, allowing you to compare, analyze, and optimize paths and movements in real-world applications and are available in MySQL Community and Enterprise Editions and HeatWave MySQL.
