Things break. So are the hard drives and SSDs. We are storing our important data on devices that we know they eventually break, so we need some protection.
We use RAID technology for granted without knowing much about its internals. This post is an attempt to explain how RAID-5 recovers data by using elementary school math. Understanding the internal will help you understand why the RAID layout with a lot of drives would take longer to recover data.
In this post, I will recap RAID-4 and RAID-5, then talk about the math behind the RAID-5. Then I will talk about the reason why we can’t change the location of hard drives or SSDs after we configure a RAID.
What are RAID-4 and RAID-5?
Let me summarize what RAID-4 and RAID-5 configurations are.
What is RAID-4?
To understand RAID-5, you first need to understand RAID-4. With RAID-4, we take the data written to disk 1, 2, and 3 and calculate the parity. We use a dedicated drive to store parity in RAID-4. Therefore, we have some drawbacks:
- Every write requires a write to the parity drive.
- Paritiy drive performance caps overall performance.
- We need to read all date from other drives to recovery parity.
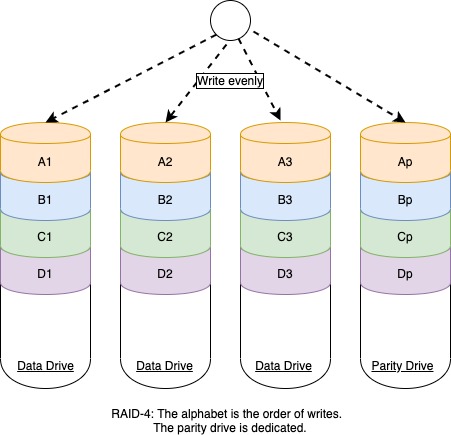
When you are reading data, you need to read all the data drives to access the data because pieces of data are spread across the drives.
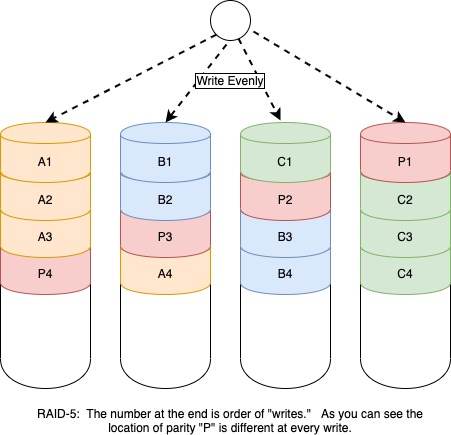
What is RAID-5?
RAID-5 fixed the shortcomings of RAID-4 by changing the parity drive at every write. For understanding the data recovery in RAID, you can consider RAID-5 as RAID-4 for now.
Why Can We Recover Data?
In order for us to understand why we can recover your data, let’s take a detour to do a simple calculation. Can you tell me the answer to P?
|
|
The answer is 6. Now, what is the value of “a“?
|
|
The answer is 1. You did something like 6 – (2+3). It means you did a subtraction. This demonstrates that if we calculate the P beforehand, then we can calculate the value of a by doing a simple subtraction. Let’s rephrase the above using by a, b and c so that we are less focused on the actual values.
|
|
Suppose a, b and c are the part of data, and we calculate P in advance and consider the P as parity. This means that when the drive breaks and we need to calculate, we can use b, c, and subtracting from P to recover a.
In this discussion, we used simple addition and subtraction. In actual implementation, we use binary numbers and the XOR operator. XOR or exclusive-OR is an operator to generates 0 when two values are the same, and 1 when two values are different. Because of the nature of binary numbers, XOR makes it easy for the developers to code addition and subtraction. Besides this implementation detail, we are using simple addition and subtraction to recover your data.
Also note that you need all available data from b, c, and P to recover data. In the worst-case scenario, we have to read all available data from all drives to recover the data for a broken or replaced drive. This is the reason recovery time grows when the number of disks grows in RAID-5. This is also precisely why we divide drives into groups of RAID-5 and stripe the data among the RAID groups.
Why Drives Can’t Be Swapped?
Since we understand how we recover your data, let’s do another simple math. I am using the same letters from the previous equation.
|
|
If you enter actual numbers such as 1, 2, and 3, you understand that both 1 + 2 + 3 and 2 + 1 + 3 are both equal to 6. Swapping the position of the numbers won’t change the answer when we are adding. While this is handy for calculation, it is problematic when implementing the RAID. There is no way for us to tell mathematically if a and b are swapped from numbers in our hands. Therefore, in actual implementation, we designate a, b and c to each device and its location. In LSI RAID, we call the order of device location “piece order.” The piece order is assigned when we configure a RAID.
There is no way for us to tell if the piece order change as long as using simple math that we use for RAID-5.
It is my understanding that there are some storage devices out there that have “piece order” written to the device itself, but generally swapping the drives will corrupt your data.
When RAID-5 Can’t Recover Your Data?
You can’t recover your data when more than two drives break. Let’s revisit our first equation.
|
|
Of course, P is 6.
Now, suppose two drives break, and we name the unrecovered values to x and y. We have no way of calculating x and y without having another formula that tells us their relationship.
|
|
This is the reason that we can’t recover data when more than two drives fail in the RAID-5 configuration.
Summary
We learned:
- We used a peculiar operator (XOR), yet we basically store the sum of data as parity.
- When a disk breaks, we can recover the data from the parity and the remaining data.
- There is no way to detect the disk swap. Therefore, we have to designate the location for each device in a RAID array.
References
The Mathematics of RAID-6, H. Peter Anvin, December 20, 2011(PDF)
