Classification of the compression algorithms.
Big Data term supposes to store and handle huge amount of data. Big Data technologies like Hadoop allow us to scale out storage and processing layers. It’s easy to scale your system – just buy new servers and add them to cluster. But before buying new hardware or delete historical data it is a good idea try to reorganize storage, specifically compress data. I’m sure that many of you heard about different compression programs that are available on Linux or Windows like gzip, zip, bzip2 and so on. Some of you know about different compression codec, like org.apache.hadoop.io.compress.GzipCodec or org.apache.hadoop.io.compress.BZip2Codec, that are supplied with many Hadoop distributions. But it’s really curiously to understand what is under the hood of this codecs and which algorithms and tricks are using for achieving better performance or compress rate. I was wondering of this and found a perfect picture here that illustrate hierarchy of the compression codec’s world:
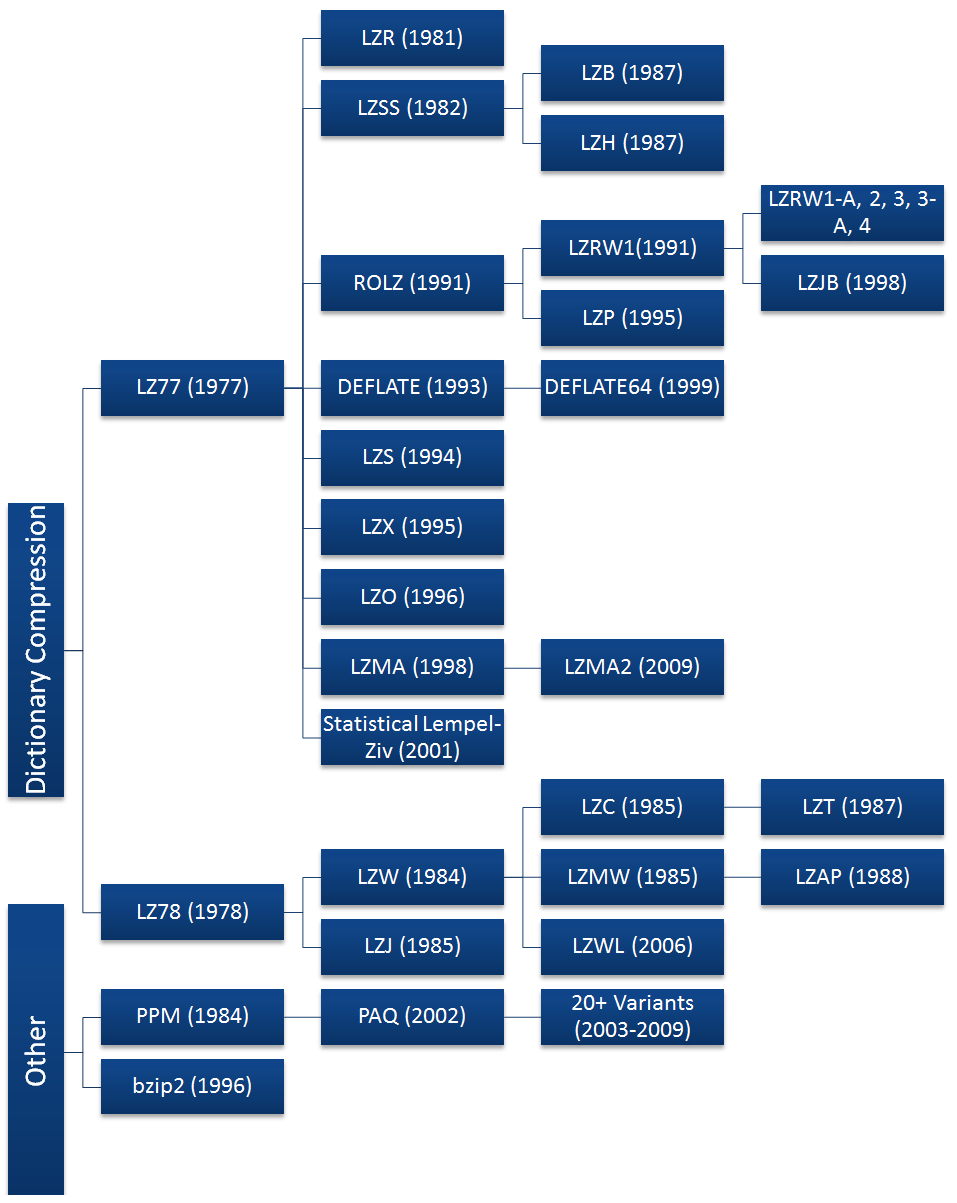
This picture shows us that most of the algorithms based on LZ77 and LZ78 (both of them are dictionary algorithms). Bzip2 has a bit different approach. Let’s have a look on the some basis concepts (let’s say building blocks) which are used for creating concrete compression algorithm.
Huffman coding
Huffman coding is one of the fundamental and one of the most efficient approach for compress data. The obvious think that we could do during
encoding alphabet is to assign some equal number of the bits for each symbol, which enough for definite encoding. But even in general case when English text are encoding, frequency occurrence of each symbol is not equal. I got from Wikipedia diagram frequency of occurrence of every English symbol:
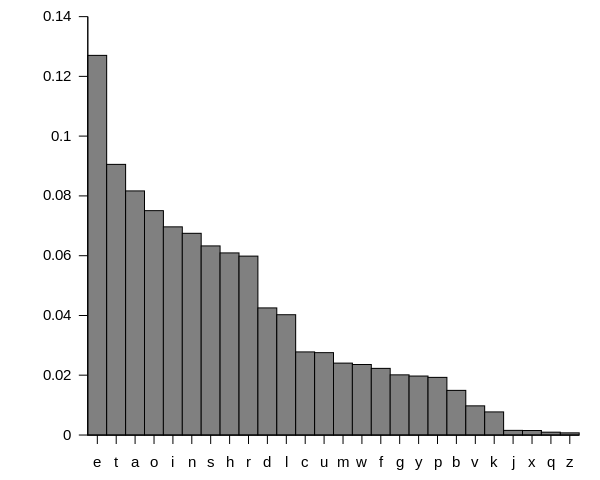
This graph shows us that probability to meet “z” (0.074%) much less than probability to meet “e” (12.702%). This fact make obvious thing that it would be useful to use variable-length encoding, like dedicate three bits for “e” – 100, and 9 bits for “z” – 001001000, instead allocating same length code for frequent and rare symbol. Its general idea of Huffman’s algorithm – more frequent symbol should to have shorter bit code. Also Huffman coding proposes how to solve this practically. Input text tokenized by symbol and calculated frequency of every symbol in this text. On the second step, we create Huffman tree – on the bottom we put two rarest symbols. They will have longest code. After this we calculate sum of this two symbols and join it with third rarest symbol. Zero bit is assign for branch that has less number (sum of the two elements compare with the frequncy of the next element). This operation are continues until we reach the top frequent symbol. I’m not sure that this explanation is clear and obvious for everybody, but hope that next example will change this. Let’s imagine that we have some text which has follow frequency of symbols occurrence:
| Letter | Z | K | M | C | U | D | L | E |
| Frequency | 1 | 7 | 24 | 32 | 37 | 42 | 42 | 120 |
Most rare symbol is “Z”, next one from the end is “K”. Z happens 2 times, “K” – 7. Sum is 9 it’s less than 24 – occurrence of the “M” symbol which is following by “K”. Put 0 bit for the less branch… after accomplishing all steps for all symbols, we could observe follow tree:
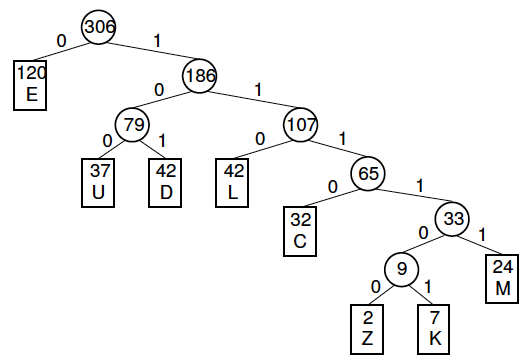
For calculating code from each symbol we have to follow from the head of the tree to the symbol’s position. For example, “K” would be encoded like 111101:
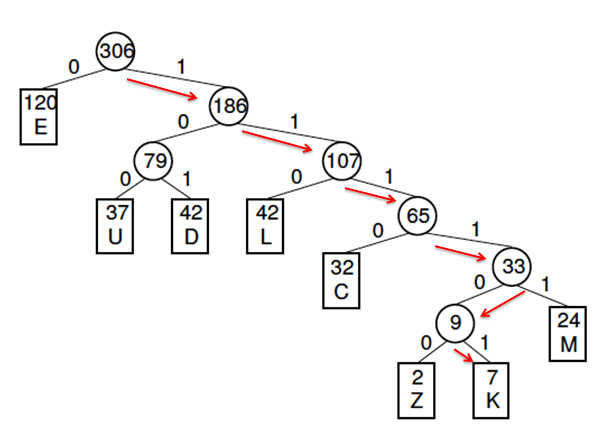
Next step is just writing down all this chains into single table:
| Letter | Freq | Code | Bits |
| E | 120 | 0 | 1 |
| D | 42 | 101 | 3 |
| L | 42 | 110 | 3 |
| U | 37 | 100 | 3 |
| C | 32 | 1110 | 4 |
| M | 24 | 11111 | 5 |
| K | 7 | 111101 | 6 |
| Z | 2 | 111100 | 6 |
For more frequent symbol (“E”) we will use 1 bit, for less frequent 6. This method successfully used in gzip codec. The big think that Huffman code is adaptive and depends on concrete data set.
Burrows–Wheeler transform (BWT)
The Burrows–Wheeler transform is an algorithm used in data compression techniques. When a character string is
transformed by the BWT, the transformation permutes the order of the characters. If the original string had several substrings that occurred often, then the transformed string will have several places where a single character is repeated multiple times in a row. The output is easier to compress because it has many repeated characters. For example (taken from Wikipedia), if we have follow input string “SIX.MIXED.PIXIES.SIFT.SIXTY.PIXIE.DUST.BOXES”, BWT(string)=”TEXYDST.E.IXXIIXXSSMPPS.B..E.S.UESFXDIIOIIIT”. Best description of this algorithm as well as example I found in Wikipedia:
“The transform is done by sorting all rotations of the text into lexographic order, by which we mean that the 8 rotations appear in the second column in a different order, in that the 8 rows have been sorted into lexicographical order. We then take as output the last column:”
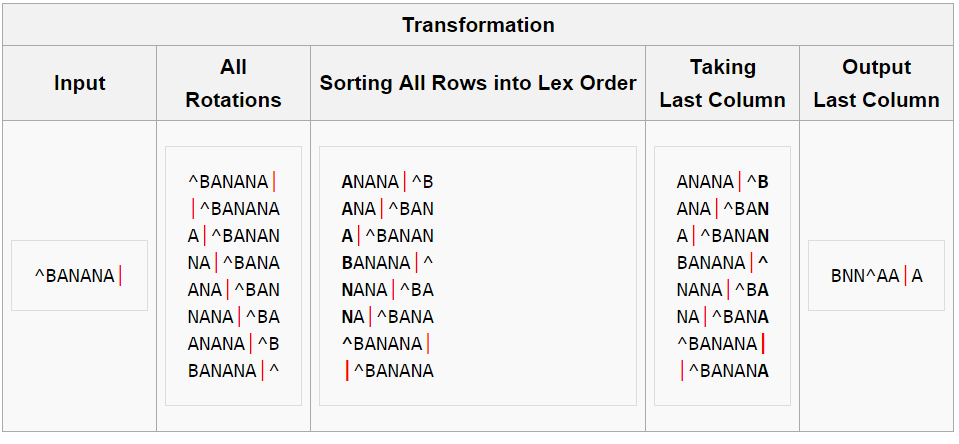
I would emphasize that this is not full algorithm for some compression codec, it’s just the way to prepare data for more efficient compression.
Move-to-front (MTF) transformation
Couple paragraphs above, we have learned (or remembered) what is the Huffman coding is. And it’s obviously very efficient algorithm for dataset where frequency of appearance of each symbol is different. But what is we have text like this “bbbbbcccccdddddaaaaa” From Mr.Huffman’s perspective it’s pretty unuseful – probability for each symbol is equal. But this dataset seems promising. Move-to-Front transformation allows us to use benefits of this text. The main idea of this method is that each symbol in the data is replaced by its index in the stack of “recently used symbols”. For example, long sequences of identical symbols are replaced by as many zeroes, whereas when a symbol that has not been used in a long time appears, it is replaced with a large number. For this transformation we have to write alphabet in lexicographical order for first iteration and mute it during the transformation. Here is example:
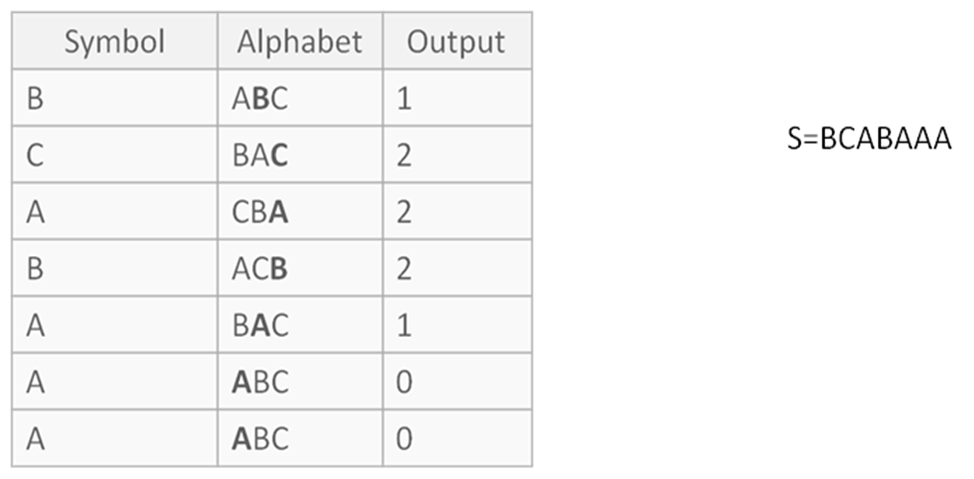
This method makes it easy to convert the data saturated long repeats of different symbols in the data block, the most frequent of which symbols are zeros. Especially suitable after BWT. If we will return to our example, where MTF(bbbbbcccccdddddaaaaa)=10000200003000030000. Transformed dataset is very efficient for Huffman coding:
| Symbol | Frequncy | Probability | Huffman code |
| 0 | 16 | 0.8 | 0 |
| 1 | 2 | 0.1 | 10 |
| 2 | 1 | 0.05 | 110 |
| 3 | 1 | 0.05 | 111 |
LZ77
This algorithm was invented in 1977 and lies in the foundation of many modern compression algorithms. For considering this algorithm I want to introduce the basic terms.“Search Buffer (Dictionary)” – part of the data that was already read. This piece represent dictionary and data from “look ahead buffer” refers to this part.
|
|
|
|
|
|
|
|
|
| Search buffer (Dictonary) |
Look ahead buffer |
||||||
<———– Direction of text movement
The basic idea is to encode the sequence of elements in Look ahead buffer (scanning stream) by link to Search buffer (dictionary), where this symbols already been used.
Key points:
– Dictionary based algorithm
– Dictionary is variable (different for every symbol), “slide window” used for creating it (search buffer).
– As soon as dictionary is variable, offset is using for linking (jump back from cursor
position to …)
– Look ahead buffer used for keep elements that are going to be encoded
– Size of look ahead buffer usually much smaller then Search buffer
– Decoding
LZ77 easier for their preparation, as do not need to search the dictionary. For me personally was very useful to have an example of this algorithm.
By algorithm, we have defined that Search buffer = 8 bytes, Lookahead buffer = 4 bytes
Step1. Search Buffer (Dictionary) is empty. Just write output in format: number of position back where this matching is, offset of matching and
next character. As soon as we don’t have matching set 0 as offset and position back and next character is “C” itself:
| Position |
Offset |
Next |
| 0 |
0 |
C |
| 8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
C |
O |
M |
P |
U |
T |
E |
R |
C |
O |
M |
A |
U |
Search buffer <———– Look ahead buffer
Step2. Move one symbol in search buffer and now dictionary contains one symbol. Whole input string contains other “C” symbol, but it’s out of “lookahead buffer”, which consists only “OMPU”. Among “OMPU” there is no matching with “C”, and it’s why we set 0 for position back and offset and “O” like next symbol:
| 8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|||||||||||||
|
|
|
|
|
|
|
|
C |
O |
M |
P |
U |
T |
E |
R |
C |
O |
M |
A |
U |
|
Search buffer <———– Look ahead buffer
| Position |
Offset |
Next |
| 0 |
0 |
O |
Step3. Search buffer is “CO”, look ahead buffer is “MPUT”. No matching.
|
|
|
|
|
|
|
C |
O |
M |
P |
U |
T |
E |
R |
C |
O |
M |
A |
U |
|
|
Search buffer <———– Look ahead buffer
| Position |
Offset |
Next |
| 0 |
0 |
M |
Step4. Search buffer is “COM”, look ahead buffer is “PUTE”. No matching.
|
|
|
|
|
|
C |
O |
M |
P |
U |
T |
E |
R |
C |
O |
M |
A |
U |
|
|
|
Search buffer <———– Look ahead buffer
| Position |
Offset |
Next |
| 0 |
0 |
P |
Step5. Search buffer is “COMP”, look ahead buffer is “UTER”. No matching.
| 8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|||||||||||||
|
|
|
|
|
C |
O |
M |
P |
U |
T |
E |
R |
C |
O |
M |
A |
U |
|
|
|
|
Search buffer <———– Look ahead buffer
| Position |
Offset |
Next |
| 0 |
0 |
U |
Step6. Search buffer is “COMPU”, look ahead buffer is “TERC”. We have match “C” into “Search Buffer” and “Look ahead buffer”:
| 8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|||||||||||||
|
|
|
|
C |
O |
M |
P |
U |
T |
E |
R |
C |
O |
M |
A |
U |
|
|
|
|
|
Search buffer <———– Look ahead buffer
But let’s try to find longer match chain, move on one symbol more:
Search buffer is “COMPUT”, lookahead buffer is “ERCO”. We have to match of small chains, which consists two symbols “CO”:
| 8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|||||||||||||
|
|
|
C |
O |
M |
P |
U |
T |
E |
R |
C |
O |
M |
A |
U |
|
|
|
|
|
|
Search buffer <———– Look ahead buffer
Let’s try to find longer chain:
| 8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|||||||||||||
|
|
C |
O |
M |
P |
U |
T |
E |
R |
C |
O |
M |
M |
A |
U |
|
|
|
|
|
|
Search buffer <———– Look ahead buffer
Search buffer is “COMPUTE”, lookahead buffer is “RCOM”. Every movement brings us positive news! Matching of the three-character chain! Move on one symbol more:
| 8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|||||||||||||
| C |
O |
M |
P |
U |
T |
E |
R |
C |
O |
M |
A |
U |
|
|
|
|
|
|
|
|
Search buffer <———– Look ahead buffer
Now miss. Let’s write what we have – if we will jump back on 8 symbols, we will have found 3 repeatable symbols and next for them will be “A” symbol:
| Position |
Offset |
Next |
| 8 |
3 |
A |
Step7. Now part of our input string lies out of a dictionary and we have there only “UTERCOMA”. Look ahead buffer has only one character “U”. it has matched and let’s write this:
| 8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|||||||||||||
| U |
T |
E |
R |
C |
O |
M |
A |
U |
|
|
|
|
|
|
|
|
|
|
|
|
Search buffer <———– Look ahead buffer
| Position |
Offset |
Next |
| 8 |
1 |
So, our output string will looks like: (00C)(00O)(00M)(00P)(00U)(83A)(81). This example doesn’t show benefits of this compression algorithm, it shows general principles of the LZ77 algorithm.
Compression codecs.
Most famous compression codecs usually based on general algorithms, like LZ77 or Huffman coding and represent some enhancement of it or combination of few compression algorithms. Like an example let’s consider most popular codecs that are using with Hadoop:
Bzip2 initially use Burrows–Wheeler transformation for changing input dataset and put more repeated symbol one by one, then apply move-to-front
algorithm changing text entropy and after move-to-front transformation apply Huffman coding. Very complex, but very efficient!
Gzip is the combination of LZ77 and Huffman coding.
Snappy, LZO, LZ4 are some variation of LZ77.
Hadoop codecs average values and expectations.
One of most common questions is “what is the average compress rate into Hadoop?”. And the best answer would be “try on your own dataset”. Average compression rate would be very different and vary within very wide diapasons. A test is it’s really easy, even if you don’t have existing Hadoop cluster. You could get VM with pseudo distributed Hadoop installation, like this, upload datafile into HDFS, create over it hive external table, then create the script with following content:
#!/bin/bash hadoop fs -rm -R /tmp/compress_bench/ hadoop fs -mkdir /tmp/compress_bench/ hive -e 'drop database testcompress cascade;' hive -e 'create database testcompress;' hive -e ' use testcompress; set hivevar:tablename='$*'; set hive.exec.compress.output=false; CREATE TABLE test_table_nocompress ROW FORMAT DELIMITED FIELDS TERMINATED BY "," LINES TERMINATED BY "\n" STORED AS TEXTFILE LOCATION "/tmp/compress_bench/test_table_nocompress" as select * from ${tablename};' hive -e ' use testcompress; set hivevar:tablename='$*'; set hive.exec.compress.output=true; set io.seqfile.compression.type=BLOCK; set mapreduce.output.fileoutputformat.compress.codec=org.apache.hadoop.io.compress.BZip2Codec; CREATE TABLE test_table_bzip2 ROW FORMAT DELIMITED FIELDS TERMINATED BY "," LINES TERMINATED BY "\n" STORED AS TEXTFILE LOCATION "/tmp/compress_bench/test_table_bzip2" as select * from ${tablename}; CREATE TABLE test_table_rc_bzip2 STORED AS RCFILE LOCATION "/tmp/compress_bench/test_table_rc_bzip2" as select * from ${tablename};' hive -e ' use testcompress; set hivevar:tablename='$*'; set hive.exec.compress.output=true; set io.seqfile.compression.type=BLOCK; set mapreduce.output.fileoutputformat.compress.codec=org.apache.hadoop.io.compress.GzipCodec; set parquet.compression=GZIP; CREATE TABLE test_table_gzip ROW FORMAT DELIMITED FIELDS TERMINATED BY "," LINES TERMINATED BY "\n" STORED AS TEXTFILE LOCATION "/tmp/compress_bench/test_table_gzip" as select * from ${tablename}; CREATE TABLE test_table_rc_gzip STORED AS RCFILE LOCATION "/tmp/compress_bench/test_table_rc_gzip" as select * from ${tablename}; CREATE TABLE test_table_pq_gzip STORED AS PARQUETFILE LOCATION /tmp/compress_bench/test_table_pq_gzip" as select * from ${tablename};' hive -e ' use testcompress; set hivevar:tablename='$*'; set hive.exec.compress.output=true; set io.seqfile.compression.type=BLOCK; set mapreduce.output.fileoutputformat.compress.codec=org.apache.hadoop.io.compress.SnappyCodec; set parquet.compression=SNAPPY; CREATE TABLE test_table_snappy ROW FORMAT DELIMITED FIELDS TERMINATED BY "," LINES TERMINATED BY "\n" STORED AS TEXTFILE LOCATION "/tmp/compress_bench/test_table_snappy" as select * from ${tablename}; CREATE TABLE test_table_rc_snappy STORED AS RCFILE LOCATION "/tmp/compress_bench/test_table_rc_snappy" as select * from ${tablename}; CREATE TABLE test_table_pq_snappy STORED AS PARQUETFILE LOCATION "/tmp/compress_bench/test_table_pq_snappy" as select * from ${tablename}; ' hive -e ' use testcompress; set hivevar:tablename='$*'; set hive.exec.compress.output=true; set io.seqfile.compression.type=BLOCK; set mapreduce.output.fileoutputformat.compress.codec=org.apache.hadoop.io.compress.Lz4Codec; CREATE TABLE test_table_lz4 ROW FORMAT DELIMITED FIELDS TERMINATED BY "," LINES TERMINATED BY "\n" STORED AS TEXTFILE LOCATION "/tmp/compress_bench/test_table_lz4" as select * from ${tablename}; CREATE TABLE test_table_rc_lz4 STORED AS RCFILE LOCATION "/tmp/compress_bench/test_table_rc_lz4" as select * from ${tablename};' hive -e ' use testcompress; set hivevar:tablename='$*'; set hive.exec.compress.output=true; set io.seqfile.compression.type=BLOCK; set mapreduce.output.fileoutputformat.compress.codec=com.hadoop.compression.lzo.LzopCodec; CREATE TABLE test_table_lzo ROW FORMAT DELIMITED FIELDS TERMINATED BY "," LINES TERMINATED BY "\n" STORED AS TEXTFILE LOCATION "/tmp/compress_bench/test_table_lzo" as select * from ${tablename}; CREATE TABLE test_table_rc_lzo STORED AS RCFILE LOCATION "/tmp/compress_bench/test_table_rc_lzo" as select * from ${tablename};' hadoop fs -du -h /tmp/compress_bench;
and finally, run this script
$ chmod +x compress_bench.sh $ nohup ./compress_bench.sh SCHEMA_NAME.TABLE_NAME > compress_bench.log &
this scripts will show you compression rate which is applicable to your data (you could find it in compress_bench.log file). I’ve asked few of our key Global DataWarehouse Leaders customers to do the same test on their real dataset to get average values. The proper way is to compare data source size with compression, but all these guys has different data source (someone has already compressed data) and for comparing apple with apple I add in the script step where created CVS file with “,” delimiter and I calculate compression rate like proportion between size of this table and target compression codec + file format. Before publish results I want to say many thanks for people who helped me to collect these statistics. It’s really great that I personally know people, who are ready to spend own time just because of love technologies! Thank you, my enthusiastic friends! And this is the result:
Text files (CSV with “,”delimiter):
| Codec Type | Average rate | Minimum rate | Maximum rate |
| bzip2 | 17.36 | 3.88 | 61.81 |
| gzip | 9.73 | 2.9 | 26.55 |
| lz4 | 4.75 | 1.66 | 8.71 |
| snappy | 4.19 | 1.61 | 7.86 |
| lzo | 3.39 | 2 | 5.39 |
RC File:
| Codec Type | Average rate | Minimum rate | Maximum rate |
| bzip2 | 17.51 | 4.31 | 54.66 |
| gzip | 13.59 | 3.71 | 44.07 |
| lz4 | 7.12 | 2 | 21.23 |
| snappy | 6.02 | 2.04 | 15.38 |
| lzo | 4.37 | 2.33 | 7.02 |
Parquet file:
| Codec Type | Average rate | Minimum rate | Maximum rate |
| gzip | 17.8 | 3.9 | 60.35 |
| snappy | 12.92 | 2.63 | 45.99 |
This results once again illustrate fact that you have always do benchmark your data compression rate. For example for bzip2 average compression rate is about 17, but some kind of data could be compressed with a rate about 60, some data types could have only 4.
Common trends.
Like a general trend, I would note some obvious things. For example, if you have sparse logs with a lot of nulls and a lot of repeated values – most probably you will have very good compression rate. Machine data (generated by ATM, sensors) also has good compression rate. Flat text (like SMS, forum capture…) usually has 2-3 times worse compression rate almost for all codecs. But all rules has an exception and as I mentioned before, the best way to know your numbers for your data is a benchmark.
Default codec.
After a quick analysis of the results, you may conclude that bzip2 have to be “default” codec almost always and it’s senseless to use codecs like gzip, snappy or lz4. But this is not entirely true. Actually, bzip2 usually has better compression rate, but as you could remember from the beginning of this article – bzip2 is not dictionary algorithm and it performs a lot of transformation (like BWT, MTF, Huffman coding) and sorting them, it cause why it much slower than others codecs for compression and decompression. Gzip seems like next “default” codec, but it’s not a splittable codec, what means if we have one 10GB file it would be processed within single Mapper like one input split and we lose parallel benefits. Snappy, LZ4 are splittable but has worse compression ratio. You should always try to find a tradeoff between this restrictions and capabilities. More details about this you will find in my
next blogposts about compression.
